Investigation and student accountability is extremely important in education today. Students need to be challenged! They will learn so much more by discovering the formulas rather than me just placing the formula on the board!
While talking to my intern about not finding anything cool dealing with recursive sequences, I got an idea. I wanted my kids to find a pattern and develop the arithmetic and geometric recursive formulas using the information that they already know.
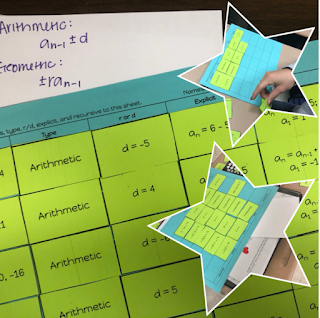
I created a cut and paste activity where students had to match the sequence, the type, the common difference/ratio, the explicit formula, and the recursive formula. From that, I hoped that students would be able to see a pattern! On a note card, I had them answer three questions...describe any patterns that you see, write a general recursive arithmetic formula, and write a general recursive geometric formula.
The students did an awesome job until they were asked to produce the general recursive formula. Arithmetic - an = an-1 + d and Geometric - an = r(an-1). I modified the lesson to give a little more direction, but not too much! I enjoyed watching the students struggle and then finally seeing the relationship. Not only was this a discovery lesson, it also provided much needed practice.
Update: My students saw a new pattern today when we started going over the formulas...They saw how simple recursive formulas are for arithmetic and geometric. They finally recognized that they were doing this all along...adding/subtracting or multiplying/dividing to find the next term. Since this was the first time that I did this activity, I feel that my students caught on a little faster to recursive formulas...typically the notation scares my students, but once they realized how it relates, I feel like they understood the concept better.
As this was the first time that I tried this activity, I am totally open to any suggestions! Thanks!
Here is my discovery lesson: Arithmetic & Geometric Recursive Investigation
~RJ
While talking to my intern about not finding anything cool dealing with recursive sequences, I got an idea. I wanted my kids to find a pattern and develop the arithmetic and geometric recursive formulas using the information that they already know.
I created a cut and paste activity where students had to match the sequence, the type, the common difference/ratio, the explicit formula, and the recursive formula. From that, I hoped that students would be able to see a pattern! On a note card, I had them answer three questions...describe any patterns that you see, write a general recursive arithmetic formula, and write a general recursive geometric formula.
The students did an awesome job until they were asked to produce the general recursive formula. Arithmetic - an = an-1 + d and Geometric - an = r(an-1). I modified the lesson to give a little more direction, but not too much! I enjoyed watching the students struggle and then finally seeing the relationship. Not only was this a discovery lesson, it also provided much needed practice.
Update: My students saw a new pattern today when we started going over the formulas...They saw how simple recursive formulas are for arithmetic and geometric. They finally recognized that they were doing this all along...adding/subtracting or multiplying/dividing to find the next term. Since this was the first time that I did this activity, I feel that my students caught on a little faster to recursive formulas...typically the notation scares my students, but once they realized how it relates, I feel like they understood the concept better.
As this was the first time that I tried this activity, I am totally open to any suggestions! Thanks!
Here is my discovery lesson: Arithmetic & Geometric Recursive Investigation
~RJ

What information did your students already know about arithmetic and geometric sequences before they did this activity?
ReplyDeleteOver the past week, we have discussed basically everything with arithmetic and geometric sequences. We had already discussed how to determine arithmetic & geometric sequences, how to find the common difference/ratio, and how to write in explicit form. So, basically, they used the list of terms to fill in the chart with the exception of the recursive. They knew how to solve for the list of terms given the recursive, but didn’t know how to write the recursive given the sequence. So, basically, they worked backwards from the recursive to get the list of terms. So that’s what I wanted them to learn from this activity is how to write the recursive given the sequence. :)
Delete